Stability

Instabilities occur whenever a joint can deflect or rotate without limit.  Put another way; a joint is unstable if there is nothing to restrain it.

With that one statement you can understand and resolve any instability problem. Instabilities are easy to understand and easy to fix. The next section explains what RISA-2D does with instabilities. The following sections provide some simple examples of instabilities and their resolution.

For additional advice on this topic, please see the RISA Tips & Tricks webpage at risa.com/post/support. Type in Search keywords: Instabilities.

Instability Procedure

Because many instabilities are inconsequential to the results yet they prevent a solution RISA-2D locks them as they are discovered and proceeds with the solution.  This locking is a boundary condition that removes the degree of freedom from the solution.  A reaction (if any) is not calculated and that is one of the dangers of ignoring instabilities.  See Testing Instabilities to learn how to test if an instability is affecting the results.

At the end of the solution you will be notified that joints have been locked and that you may view the affected joints in a model view.  These locks will also be reported in the Reactions spreadsheet.

Note

• Isolated rotational instabilities do not produce a notification that joints have been locked.  You may adjust this in the Output section of the Application Settings on the Tools menu if you wish to be warned about all instabilities. The warning for rotational instabilities looks like below:

Instability Causes

Common causes of instabilities are briefly mentioned here and then highlighted in the examples below.

Member End Releases – Boundary Conditions

Overuse of member end releases and/or boundary conditions is by far the most common cause of instability as shown in the examples below.  The solution is to either remove a member end release or change a boundary condition so that the joint is restrained.  At least one member or boundary needs to be fixed to each joint to prevent instability.  If you think of a joint as the end of a member and specify no release for that member end this member still will not experience moment at the end if all other elements are left unfixed.

Unconnected Elements

Joints that are not connected into the model cause instabilities.  This is much more common in models without Physical Members as can be seen below.  The solution may be to merge the model with the model merge feature.

Flexible Elements

Members or plates with relatively small properties such as a long member with a moment of inertia of 1.0 in⁴ can cause instabilities.  This is usually not a problem unless the members are not used properly.

Instability Examples

These simple examples are provided to directly address the common scenarios that occur in structural modeling.  You will notice a recurring theme so once you understand one or two of them you will have a handle on the causes and resolutions for most instabilities, including those in more complex models.

Remember the golden rule as you look at each example:  A joint is unstable if there is nothing to restrain it.

Cantilever Beam/Column

If a member end release is specified at the free end of a cantilever the joint becomes unstable because it is free to rotate without any resistance.

Cause:  Specifying a member release at the free end of a cantilever member.

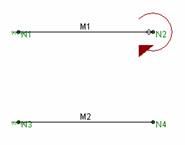
Resolution:  Remove the member end release.

If the member is not released from the joint then the member provides resistance to the joint so that it cannot rotate without limit.  The member end moves and rotates and the joint goes along for the ride.  There will be no moment at the free end of the member since there is nothing there to pass moment.

Column at a Support

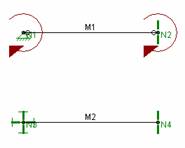
If a pinned column base is modeled with a pinned boundary condition AND a member end release at the base of the column the joint becomes unstable because it is free to rotate without any resistance.

Cause:  Specifying a pinned boundary condition AND a member release.

Resolution:  Either remove the member end release or specify a fixed boundary condition.  Do not do both unless you want a fixed column base that resists moment.

If the member is not released from the joint then the member provides resistance to the joint so that it cannot rotate without limit.  The member end rotates and the joint goes along for the ride.  There will be no moment at the base of the member since the pinned boundary cannot resist moment.

If instead the boundary is specified as fixed then the boundary provides resistance to the joint so that it cannot rotate.  The member end release allows it to rotate while the joint does not.  There will be no moment at the base of the member since the fixed boundary cannot pass moment through the member end release.

Simply Supported Beam

If a pinned beam end is modeled with a pinned boundary condition AND a member end release the joint becomes unstable because it is free to rotate without any resistance.

Cause:  Specifying a pinned boundary condition AND a member release.

Resolution:  Either remove the member end release or specify a fixed boundary condition.  Do not do both unless you want a fixed member end that resists moment.

If the member is not released from the joint then the member provides resistance to the joint so that it cannot rotate without limit.  The member end rotates and the joint goes along for the ride.  There will be no moment at the end of the member since the pinned boundary cannot resist moment.

If instead the boundary is specified as fixed then the boundary provides resistance to the joint so that it cannot rotate.  The member end release allows it to rotate while the joint does not.  There will be no moment at the end of the member since the fixed boundary cannot pass moment through the member end release.

Beam-Column Connection

If a pinned beam/column connection is modeled with a released column end AND a released beam end the joint becomes unstable because it is free to rotate without any resistance.

Cause:  Specifying a released column end AND a released beam end.

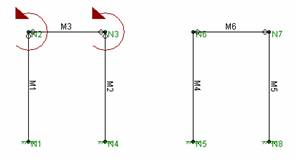
Resolution:  Either remove the column end release or the beam end release.  Do not do both unless you want a fixed connection that resists moment.

If the column is not released from the joint then the column provides resistance to the joint so that it cannot rotate without limit.  There will be no moment at the connection since the beam end release cannot pass moment.

Simple Truss

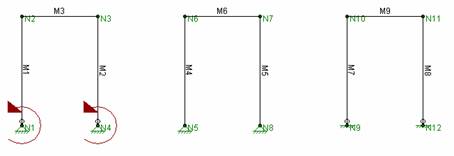
If a truss panel point is modeled with releases at the ends of EVERY member connecting to that point the joint becomes unstable because it is free to rotate without any resistance.

Cause:  Specifying all members with released ends.

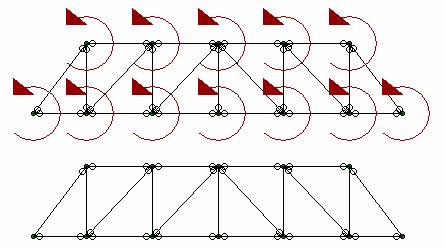
Resolution:  Either remove one end release or add a rotational boundary condition at each joint.  Do not do both.

If one member end is not released from each joint then the member provides resistance to the joint so that it cannot rotate without limit.  There will be no moment at the member end since the remaining members have end releases and cannot pass moment.

You may also solve the problem with a rotational boundary condition at each joint.  Using the ALL code you can restrain each joint for rotation and proceed to use end releases at all members.

Unconnected Elements

If a joint, member or plate is not connected to the model then there will be instability.  With the use of Physical Members this is rare in a model that only consists of beam elements however those that have plates or finite members can be defined in a way that they are not connected.

Cause:  Unconnected elements.  The portal frame is not connected to the plate elements because the bottoms of the columns do not fall on plate corners.  The plates are stable however the portal frame is not.

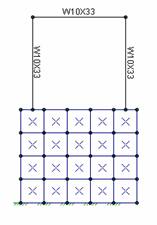
Resolution:  For beam models, run the Model Merge feature.  For plate models redefine the mesh so that plates are connected at their corners.  Model merge will not solve problems caused by lack of plate continuity.

Testing Instabilities

Although some can be ignored, keep in mind that not all instabilities are necessarily inconsequential.  Look at the following model:

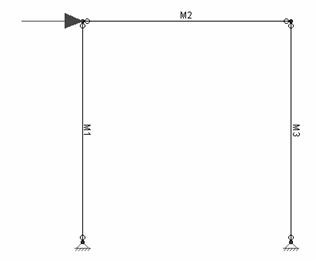
This is an example of a single bent frame that is laterally unstable.  To obtain a solution the lateral direction would be locked and a solution obtained, though not a correct one.  The warning message may be annoying if you know the instabilities being locked are of no consequence, but there won't be any surprises.

The best way to test whether an instability is inconsequential or not is to apply a Reaction to the joint in the unstable degree of freedom.  Then re-run the model and examine the reactions.  If the Reaction that is restraining the instability is showing a non-zero force or moment, then you have a problem with the model that must be corrected for you to get valid results.  If the Reaction that is restraining the instability is showing a ZERO force or moment, then the instability is inconsequential to the results.