Loads - Thermal Loads

You can model the effects of temperature differentials in members and plates. For members, these loads cause the axial expansion or contraction of the member along its length, i.e. axial stress only. The temperature is assumed constant across the member's depth. For plates, these loads cause an in-plane expansion or contraction of the plate. The temperature is assumed constant through the thickness of the plate.

Note: The internal axial deflections for beam members are the average of the end deflections for thermal loads.

Apply a Thermal Load

To apply a Thermal Load:

Select the members you wish to assign a thermal load to.
Go to the Home ribbon.

Click on image to enlarge it
Click the Line icon or the Plate Surface Load icon in the ‘Draw Loads’ section.
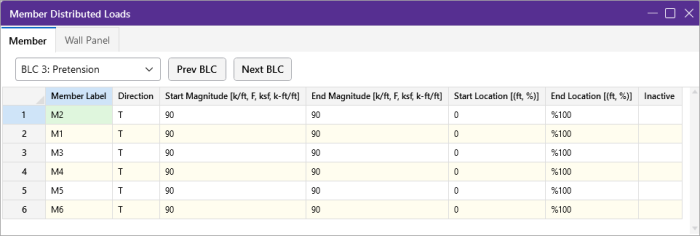
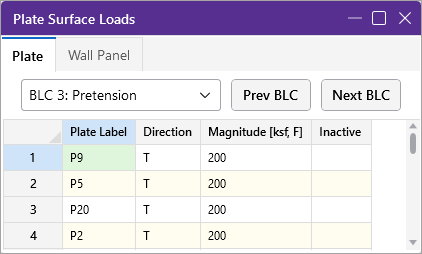
Define a distributed load with a direction of T and a magnitude, in temperature.

Note:

You may also specify or edit thermal loads in the Distributed Loads Spreadsheet or the Plate Surface Loads Spreadsheet.
An easy way to do thermal loadings is to define the joint temperatures (on the Joint Coordinates Spreadsheet) as all zero, so any defined thermal loads are the full stress inducing temperatures.

Record Thermal Loads for Members

The Coefficient of Thermal Expansion (α) is entered on the Materials spreadsheet. Note that this value is entered per 100,000 degrees (it is sometimes listed per 1,000 degrees).

The joint temperatures recorded on the Node Coordinates spreadsheet define the ambient thermal state of the structure. Thermal loads, entered as distributed loads on the Distributed Loads spreadsheet, induce axial stress in the member.

Click on image to enlarge it

The difference between the applied thermal load and the ambient temperature is the stress inducing temperature.

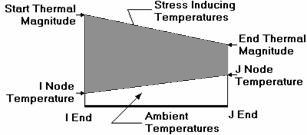
Since you can define start and end locations for the thermal load, you can define up to three separate thermal regions. Interpolating from the I-end temperature to the start thermal load for the first region, from the start thermal load to the end thermal load for the second region and from the end thermal load to the J end temperature for the third region.

Thermal Force Calculation

The joint temperatures recorded on the Node Coordinates Spreadsheet define the ambient thermal state of the structure. The joint temperature at the I-end of the member is interpolated across to the J end temperature to define the ambient state of the member. Thermal loads, entered as distributed loads on the Distributed Loads spreadsheet, induce axial stress in the member. The difference between the applied thermal load and the ambient temperature is the stress inducing temperature.

Thermal forces are calculated as follows:

Ft = A*E*a*ΔT

Where,

F_t = Calculated Thermal Force

A = Member Cross Sectional Area

E = Elastic Modulus

a = Coefficient of Thermal Expansion

ΔT = Stress Inducing Temperature

Prestressing with Thermal Loads

Thermal loads provide a way to introduce pre-stressing in a model. Given a desired prestress force, just back-solve the thermal force equation for the needed DT. Remember, as the model expands (or contracts), the prestress force may be altered.