To solve the model
The solution is based on load categories and load combinations using the widely accepted linear elastic stiffness method for solution of the model. The stiffness of each element of the structure is calculated independently. These element stiffnesses are then combined to produce the model's overall (global) stiffness matrix. This global matrix is then solved versus the applied loads to calculate point deflections. These point deflections are then used to calculate the individual element stresses. The primary reference for the procedures used is Finite Element Procedures, by K. J. Bathe (Prentice-Hall, 1996).
RISAFloor performs and analysis and design for all members defined within the program. This includes Gravity only members as well as Lateral members. The main difference between the two member functions is that the final design of Lateral members is assumed to occur in RISA-3D. Refer to the section on RISA-3D Integration for more details.
When a solution has been performed
and the results are available the “S” icon on the status bar in the
lower left corner will change from 
(gray) to 
(blue). You may then modify the design, while
maintaining the results, using the Member Redesign Dialog. See Member Redesign Dialog for more
information.
After a solution has been performed
and modifications are made to the model, the "S" icon changes to 
(yellow). This indicates that the model has been solved
but then modified. These changes may affect the results and thus another
solution may be required. The reason for this is that the stiffness and/or
weight of the modified members may have changed. While these differences
are often negligible it is a good idea to resolve the model when you are
finished modifying the designs so that the results reflect the actual
stiffness and weight.
Other changes made outside the Member Redesign Dialog, such as changes to the geometry or within the spreadsheets, cause the results to be cleared and another solution is then necessary.
When you save a file that has been solved, you may also save your results. The next time that file is opened the saved results will be opened as well. You may use the Application Settings on the Tools Menu to change the way that you are prompted to save results. See Application Settings for more information.
RISAFloor performs an independent solution at each floor. The assumptions in the Floor solution are essentially the following:
These assumptions are not always 100% accurate. Therefore, the RISA-3D solution can differ in cases where these assumptions are less than perfect.
When you include the column rotational stiffness in the RISAFloor analysis (see the setting on Model Settings), changes to the column size will affect the stiffness of the floor and the distribution of forces on that floor. Because the program performs solution for upper floors first, it is common for the original "required" size of a column at an upper level to be insufficient when the forces from the lower level are added in. The column will then be resized and the "Final Shape"doesn't match the analysis size. For this reason, the program may present the user with the following dialog.
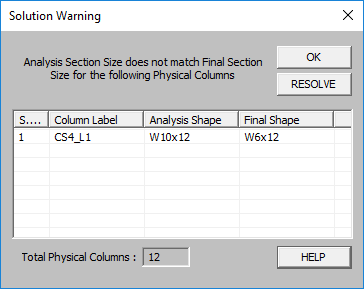
The purpose of this dialog is to ask the user if he/she wants to re-solve the model using the final shapes on those upper floor levels to see if these are going to significantly affect the beam design (or slab forces for RISAFloor ES models only).
One may choose to ignore those differences because the columns are expected to change again when the lateral analysis is performed in RISA-3D. Therefore, the column sizes are only approximations and may be perfectly acceptable without a re-analysis.
Static solutions are based on load combinations
and may be performed on any defined load combinations. When
a static solution has been performed and the results are available the to
The solution is based on the widely accepted linear elastic stiffness method for solution of the model. The stiffness of each element of the structure is calculated independently. These element stiffnesses are then combined to produce the model's overall (global) stiffness matrix. This global matrix is then solved versus the applied loads to calculate joint deflections. These joint deflections are then used to calculate the individual element stresses. The primary reference for the procedures used is Finite Element Procedures, by K. J. Bathe (Prentice-Hall, 1996).
This solution method is also sometimes referred to as an Active Column solution method. In finite element analysis, the nonzero terms of the stiffness matrix are always clustered around the main diagonal of the stiffness matrix. Therefore, the Skyline or Active Column solutions take advantage of this by condensing the stiffness matrix to exclude any zero stiffness terms that exist beyond the last non-zero term in that column of the matrix.
Since the majority of terms in a stiffness matrix are zero stiffness terms, this method greatly reduces the storage requirements needed to store the full stiffness matrix. However, for large models (+10,000 joints) , the memory requirements even for a skyline solution can be problematic.
This solution method has been used successfully in RISA for more than 20 years, and has proven its accuracy continuously during that time.
The skyline solver described above is moderately efficient because it only stores and performs operations on the terms within the "skyline" of the stiffness matrix. However, that solution still contains a great number of zero stiffness terms within the skyline of the matrix. A Sparse Solver will reduce the matrix size to an absolute minimum by eliminating the storage of ALL zero stiffness terms.
A sparse solver is the most efficient solution methodology possible because it stores and performs operation only on the non-zero terms of the stiffness matrix. For this reason the sparse solution is preferred from both a solution speed and memory requirement standpoint.
Note