Solution
To solve the model, click the 
button on the Home tab.
A progress bar displays information as the solution proceeds. In general,
loads are attributed to the slabs, beams and footings followed by an optimization of the slab reinforcement, as well as beam and footing sizes and reinforcement.
Any warnings are listed in the Warning Log, which can be opened from the
Spreadsheets Menu. For more information on how slabs and beams are optimized, see Design Optimization. For more information on footing optimization, see Footings - Results.
Solution Method
The solution is based on load categories and load combinations using the widely accepted linear elastic stiffness method for solution of the model. The stiffness of each element of the structure is calculated independently. These element stiffnesses are then combined to produce the model's overall (global) stiffness matrix. This global matrix is then solved versus the applied loads to calculate point deflections. These point deflections are then used to calculate the individual element stresses. The primary reference for the procedures used is Finite Element Procedures, by K. J. Bathe (Prentice-Hall, 1996).
When
a solution has been performed and the results are available the
icon on the status bar in the lower left corner will change from
to 
. If any changes are
made to the model that invalidate the results then the results will be
cleared and another solution will be necessary.
The specific type of solution performed by RISAFoundation is Batch Solution. This means that a solution may be performed on multiple combinations and the results retained for each solution. You may group the results by item or by load combination in the results spreadsheets by choosing the Sort by Combination or Sort by Item option on the Results ribbon. For example, you can have all the combination results for beam M1 grouped together or you can have all the beam results for Load Combination "DL+LL" grouped together. See Load Combinations to learn how to mark combinations to be solved in the batch solution.
When you save a file that has been solved, you may also save your results. The next time that file is opened, the saved results will open as well. You may use the Application Settings on the File Menu to change the way that you are prompted to save results. For more information, see Output Application Settings .
Static Solutions / Stiffness Matrix
Static solutions are based on load combinations
and may be performed on any defined load combinations. When
a static solution has been performed and the results are available the icon on the status bar in the lower left corner will change from to . If any changes are
made to the model that invalidate the results then the results will be
cleared and another solution will be necessary.
The solution is based on the widely accepted linear elastic stiffness method for solution of the model. The stiffness of each element of the structure is calculated independently. These element stiffnesses are then combined to produce the model's overall (global) stiffness matrix. This global matrix is then solved versus the applied loads to calculate joint deflections. These joint deflections are then used to calculate the individual element stresses. The primary reference for the procedures used is Finite Element Procedures, by K. J. Bathe (Prentice-Hall, 1996).
Skyline Solver
This solution method is also sometimes referred to as an Active Column solution method. In finite element analysis, the nonzero terms of the stiffness matrix are always clustered around the main diagonal of the stiffness matrix. Therefore, the Skyline or Active Column solutions take advantage of this by condensing the stiffness matrix to exclude any zero stiffness terms that exist beyond the last non-zero term in that column of the matrix.
Since the majority of terms in a stiffness matrix are zero stiffness terms, this method greatly reduces the storage requirements needed to store the full stiffness matrix. However, for large models (+10,000 joints) , the memory requirements even for a skyline solution can be problematic.
This solution method has been used successfully in RISA for more than 20 years, and has proven its accuracy continuously during that time.
Sparse Solver
The skyline solver described above is moderately efficient because it only stores and performs operations on the terms within the "skyline" of the stiffness matrix. However, that solution still contains a great number of zero stiffness terms within the skyline of the matrix. A Sparse Solver will reduce the matrix size to an absolute minimum by eliminating the storage of ALL zero stiffness terms.
A sparse solver is the most efficient solution methodology possible because it stores and performs operation only on the non-zero terms of the stiffness matrix. For this reason, the sparse solution is preferred from both a solution speed and memory requirement standpoint.
Multi-Threaded Solutions
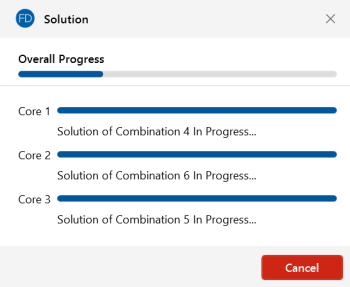
RISA products now have the ability to use multiple CPU cores if you check the check box in (Global) Model Settings. Set the Processor Core Utilization to Single, Balanced (Optimum) or Maximum in the Solution tab of Model Settings. The program will split up the solving based on load combination and use each available CPU core to solve load combinations in parallel. Once this portion of the solution is complete, the program then combines this data for enveloping and design purposes. This behavior will improve solution time for computers with multiple cores and models with large numbers of load combinations.
During the load combination portion of the solution, the Solution dialog will show progress for each core being used, as shown below:
Click on image to enlarge it